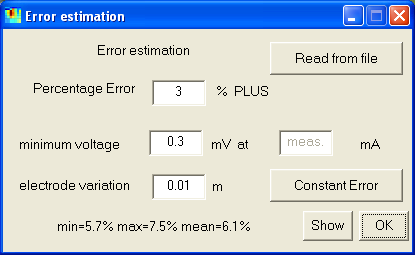
Knowing the accuracy of the data points can significantly increase the interpretation
of geophysical data. If errors (in terms of standard deviations) are not measured,
it is possible to estimate. The (relative) data erros are supposed to consist
of two parts, one percentage error plus an voltage error considering the limited
accuracy of the field equipment. The voltage error is divided by the driving
current and multiplied with the configuration factor giving large errors for
high k-values (such as dipole-dipole) and small errors for low k-values (such
as wenner).
If no errors are given in the data file, an error estimation dialog is called.
It is also possible to assume equal errors for the data or to read the standard
deviation from text file.